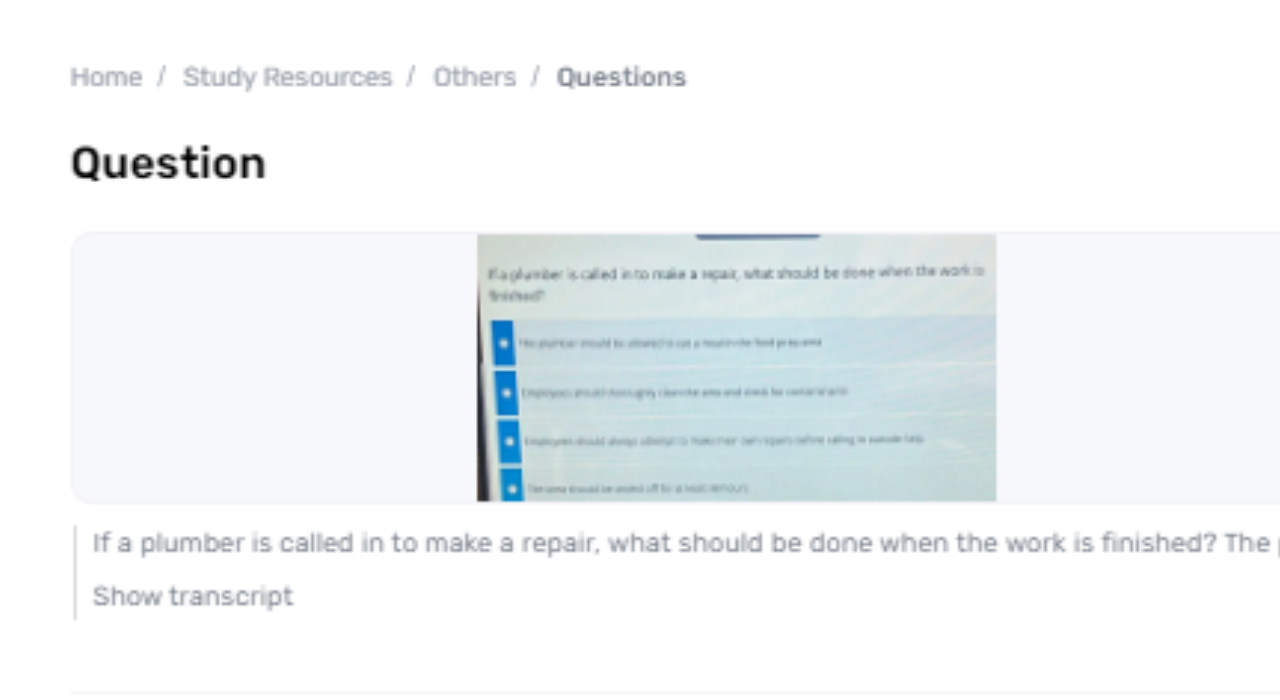
Solving conditions may be a principal aptitude in algebra that helps us get connections between factors. In this essay, we are going to address the condition 19j–18j=12, which may be a straightforward direct condition including a single variable. Despite its simplicity, understanding this condition gives a clear outline of essential arithmetical standards and problem-solving procedures. By working through this issue, able to investigate the method of confining the variable and confirming the arrangement, advertising an understanding of how fundamental logarithmic controls are connected.
Disentangling the Condition
To unravel condition 19j-18j=12, the primary step is to rearrange the expression on the cleared outside of the condition. The condition includes two terms with the variable J, which can be combined. By applying the rule of combining like terms, we subtract 18j from 19j. This operation rearranges the cleared outside of the condition as follows: 19j-18j=(19-18)j=1j In this way, the condition disentangles to: 1j=12 This disentanglement uncovers that 1j is proportionate to 12. Since duplicating or separating by 1 does not alter the esteem, we are cleared out with the disentangled condition j=12.
Confining the Variable
In variable-based math, separating the variable could be a significant step in tackling conditions. For the given condition 19j-18j=12, after rearranging, we have 1j=12. This step successfully confines the variable J on one side of the condition. In this particular case, confining J is clear since the coefficient of j is 1. In this way, the condition 1j=12 straightforwardly suggests that J equals 12. This step illustrates a key principle of variable-based math: when a variable is disconnected and contains a coefficient of 1, the arrangement is essentially the esteem on the other side of the condition.
Confirmation of the Arrangement
Confirmation is a basic portion of understanding conditions because it affirms that the arrangement fulfills the initial condition. To confirm the arrangement j=12, substitute 12 back into the first condition 19j-18j=12: 19(12)-18(12)=228-216=12 The cleared outside of the condition breaks even with 12, which matches the proper side of the condition. This affirmation confirms that our arrangement has been rectified. Confirmation guarantees that no mistakes were made amid the rearrangements and tackling forms, strengthening the precision of our arrangement.
Arithmetical Standards Outlined
This basic condition 19j-18j=12 serves as an outline of a few critical logarithmic standards. To begin with, it illustrates the concept of combining like terms, a crucial procedure in rearranging logarithmic expressions. Moment highlights the guideline of segregating a variable to discover its esteem. At last, it fortifies the significance of confirmation in affirming that an arrangement is precise. These standards are foundational to variable-based math and are appropriate to more complex issues including straight conditions and past.
Viable Applications
Understanding how to fathom straightforward conditions like 19j-18j=12 has common suggestions in different areas, counting science, designing, funding, and ordinary problem-solving. For case, in monetary arranging, understanding conditions can offer assistance decide how changes in costs or salary influence budgets. In building, conditions are utilized to unravel obscure factors in plan calculations. Mastery of logarithmic procedures, counting those illustrated by this issue, is basic for tending to real-world challenges and making educated choices.
Approach for Addressing a Gauth Address
1. Clarify the Inquiry
Determine if the issue relates to setup, operation, administration, or investigating to tailor your reply.
2. Research Essential Subtle elements
Check Gauth’s official documentation and common client issues to guarantee an accurate response.
3. Draft the Reaction
Display the data clearly and organized, giving particular steps that address the inquiry.
4. Review and Refine
Confirm the rightness of the data and adjust for clarity and conciseness, guaranteeing the reaction is simple to take after.
Conclusion
In conclusion, fathoming the condition 19j-18j=12 includes an arrangement of direct logarithmic steps that outline essential standards of variable-based math. By disentangling the condition, segregating the variable, and confirming the arrangement, we pick up knowledge into fundamental logarithmic strategies that are pertinent to more complex issues. The arrangement to the condition is j=12, and the method of understanding it strengthens key logarithmic concepts such as combining like terms and separating factors. Understanding and applying these standards are significant for handling a wide run of mathematical and down-to-earth issues, illustrating the esteem of polynomial math in both scholarly and real-world settings.